The Stopping and
Range in Compounds
(See special Request for Collaborators at bottom of page)
Soon after the discovery of energetic particle emission from radioactive materials, there was interest how these corpuscles were slowed down in transversing matter. In 1900 Marie Curie stated: "Les rayons alpha sont des projectiles materiels susceptibles de perdre de leur vitesse en traversant la mati�re." [1] Scientists realized that since these particles could penetrate thin films, experiments measuring their energy loss and scatter might finally unravel the secrets of the atom. Bragg and Kleeman started to conduct such experiments with a radium source in 1903, but were unable to find many types of thin films, since there were no "goldbeaters" in Australia. So they studied the energy loss of alpha particles in hydrocarbon gases such as methyl bromide and methyl iodide to find how alpha stopping depended on the atomic weight of the target. They removed the stopping contribution of hydrogen and carbon atoms in the hydrocarbon target gases by a subtraction of the stopping power in equivalent pure carbon and hydrogen targets. From their analysis in 1905, comes Bragg's Rule that the stopping of a compound may be estimated by the linear combination of the stopping powers of individual elements.[2]
|
Atom Stopping Simple Compounds |
|
Figure 1 |
This rule is reasonably accurate, and the measured stopping of ions in compounds usually deviates less than 20% from that predicted by Bragg's rule. The accuracy of Bragg's rule is limited because the energy loss to the electrons in any material depends on the detailed orbital and excitation structure of the matter, and any differences between elemental materials and the same atoms in compounds will cause Bragg's rule to become inaccurate. Further, any bonding changes may also alter the charge state of the ion, thus changing the strength of its interaction with the target medium.
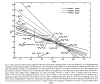
Experimental studies of Bragg's rule started in the
1960s, and wide discrepancies were found from simple additivity of stopping
powers. See Figure 1
for an example of H and C non-additivity in simple hydrocarbons.[3] In
this figure, the stopping in various hydrocarbons is taken for pairs of
compounds, and the relative contribution of H and C is extracted (solving two
equations with two unknowns). It is found that the relative contribution of H
and C differs by almost 2x over the range of compounds.
Similar work studied more complex hydrocarbons but instead of adding H and C
bonds, they added extra hydrocarbon molecules. In this study, they found that
by adding molecules to hydrocarbon strings, stopping linearity returned.[4] See Figure 2. Adding new molecules just scaled the
stopping by the extra number of atoms. These results showed that atomic bonding
had large effects on stopping powers of simple molecules while extra
agglomeration of molecules had a small stopping effect.
|
Molecule Stopping Large Compounds |
|
Figure 2 |
Since these early experiments, theorists have shown that extensive calculations can predict the stopping of light ions (usually protons) in hydrocarbon compounds. Much of this work hsa been based on a seminal paper by Peter Sigmund that developed methods to account for detailed internal motion within a medium.[5] This theory allows for arbitrary electronic configurations in the target. Sabin and collaborators used this approach to calculate stopping powers for protons in hydrocarbons with good success.[6] Sabin's calculation follows what is sometimes called the K�ln Core and Bond (CAB) approach which is discussed in detail below.
We are not going to review the complex theoretical work on stopping in compounds. Our interest is to try to find a simple way to estimate the changes that compounds introduce to the use of Bragg's rule to generate stopping powers of compounds. For the general user of SRIM, with only a minimal knowledge of the physics of stopping theory, we need a simple method to estimate bonding corrections to stopping.
The Core and Bond (CAB) approach suggested that stopping powers in compounds can be predicted using the superposition of stopping by atomic "cores" and then adding the stopping due to the bonding electrons.[7] The core stopping would simply follow Bragg's rule for the atoms of the compound, where we linearly add the stopping from each of the atoms in the compounds. The chemical bonds of the compound would then contain the necessary stopping correction. They would be evaluated depending on the simple chemical nature of the compound. For example, for hydrocarbons, carbon in C-C, C=C and C=t=C structures would have different bonding contributions (C=C indicates a double-bond structure and C=t=C is a triple bond). The contribution to stopping by a carbon atom in a C=C bond is almost twice that of a carbon atom single-bond state. And a carbon atom in a triple-bond state contributes even greater stopping powers. See Figure 3. By merely specifying the bonding of the atoms in the compound, for example, SRIM can then generate a stopping correction required for the compound with this bonding arrangement.
|
Core & Bonds |
|
Figure 3 |
SRIM uses this approach to generate corrections between Bragg's rule and compounds containing the common elements in compounds: H, C, N, O, F, S and Cl. These light atoms have the largest bonding effect on stopping powers. Heavier atoms are assumed not to contribute anomalously to stopping because of their bonds (discussed later). When you use SRIM, you have the option to use the Compound Dictionary which contains the chemical bonding information for about 150 common compounds. The compounds with corrections are shown with a Star symbol next to the name. When these compounds are selected, SRIM shows the chemical bonding diagram and calculates the best stopping correction. The correction is a variation from unity (1.0 = no correction). Notice that carbon atoms have almost a 4x change in stopping power from single bonds to triple bonds. This large change indicates the importance of making some sort of correction for the stopping of ions in compounds.
The CAB approach that SRIM uses has been tested on more than 100 compounds, from 162 experiments (discussed later). SRIM correctly predicts the stopping of H and He ions in compounds with an accuracy of better than 2% at the peak of the stopping curve, ~125 keV/u.
You can introduce other compounds to SRIM by adding
to the Compound Dictionary. You need to edit the file ..\Data\COMPOUND.dat.
Instructions are at the top of the file, and included are more than 150
examples to guide you in creating your own compounds. SRIM will use your
chemical bonding information to calculate the stopping correction. SRIM can
only calculate bonding of the seven elements: H, C, N, O, F, S and Cl. Any
other elements will be assumed to have the same stopping as in their elemental
form.
Details of how SRIM calculates the bonding correction to stopping can be found in the paper: J. F. Ziegler and J. M. Manoyan, Nucl, Inst. Methods, B35, 215-228 (1988).
[1] Mme. Pierre Curie, C. R. Acad. Sci., 130, 76 (1900).
[2] W. H. Bragg and R. Kleeman, Philos. Mag., 10, 318 (1905)
[3] A. S. Lodhi and D. Powers, Phys. Rev., A10, 2131 (1974).
[4] D. Powers, Acc. Chem. Res., 13, 433 (1980).
[5] P. Sigmund, Phys. Rev., A26, 2497 (1982).
[6] J. R. Sabin and J. Oddershede, Nucl. Inst. Methods, B27, 280 (1987).
[7] G. Both, R. Krotz, K. Lohman and W. Neuwirth, Phys. Rev., A28, 3212 (1983).

Examples of Compound Corrections
|
He into Air |
|
H into Water |
|
He into Water |
As an example of where Bragg's rule works well without correction, consider the range of He ions into air. Air is a mixture of N2, O2 and Ar, all elements which are gaseous in their normal state. So the combined stopping powers would be expected to be quite close to Bragg's rule. The plot "He into Air" shows ranges of He ions because these are more accurately measured than stopping powers for high energy light ions in gases. The citations of the plotted data are in the file "Air - He Ions" (Adobe Acrobat format). These citations date back 100 years since energetic alpha particles were available since the discovery of radioactivity. The solid line is the SRIM calculation for AIR, which uses just the Bragg additivity of ion stopping in N(76%), O(23%) and Ar(1%).
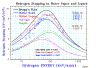
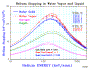
An example of where Bragg's rule fails is for water. Hydrogen undergoes a very large change in structure when it is in most compounds -- more than for any other element. Typically, hydrogen's stopping changes by up to 30% in compounds, but since its contribution to total stopping is small, hydrogen's bonding is a small change to the total stopping. Also, there is a phase change for solid water (ice) since stopping powers for H and O are most commonly measured in gaseous state, and we need stopping powers for both water vapor and water solid (ice). The plot "H into Water" shows the stopping of protons in water using simple additivity (labeled Bragg's Rule), and with the corrections from the Compound Dictionary. The data is rather erratic, but the general trends are clear. The citations of the plotted data are in the file "Water" (Adobe Acrobat format).
The plot "He into Water" shows is a similar plot for He ions into water. This data is more consistent than that for H ions, above, and it also clearly shows the "phase effect" for water in gaseous phase and for water in solid phase. All the solid lines are SRIM calculations for H, O or H2O in either gaseous or solid state. The citations for the plotted data are also found in the "Water" document.
|
He into Ethylene |
An example of a large correction is the 12% correction necessary for Ethylene, C2H4. Shown in figure "He into Ethylene (gas)" is the stopping of He ions into Ethylene showing the Bragg's rule stopping estimate for (2 Carbon) + (4 Hydrogen) atoms (black curve). These values are clearly too small. There are two corrections that must be made. The stopping of He in Carbon assumes a solid-phase target. The stopping in gas-phases usually increases the stopping. Shown in the curve is the stopping due to carbon solid (solid green line) and carbon in gas phase (dashed green line). Then we must consider the bonding effects. The ethylene molecule contains 4 H-C single bonds, and a C=C double bond. From the discussion above, the C=C bond adds significantly to the stopping power near the peak of the stopping. SRIM calculates that this increase is 8.3%. So the two corrections make the total adjustment to the stopping to be about 12%, and it brings the calculation into reasonably accurate agreement with the data. The citations of the plotted data are listed below under target of C2H4.
|
H into Styrene |
|
He into Styrene |
Another similar example of a large correction is that necessary for a target of Polystyrene, C8H8. Shown in figures "H into Styrene" and "He into Styrene" are the stopping of H and He ions into Polystyrene. They show the Bragg's rule stopping estimate for (8 Carbon) + (8 Hydrogen) atoms (black curve). These values are too small. There are two corrections that must be made. The stopping of ions in Hydrogen assumes a gas-phase target. The stopping in gas-phases has higher stopping than for solid phase. Shown in the curve is the stopping due to hydrogen in gas phase (dashed green line) and hydrogen solid (solid green line). Then we must consider the bonding effects. The Polystyrene molecule contains 8 H-C single bonds, 6 C-C single bonds, and 3 C=C double bonds (see the molecular structure in SRIM's Compound Dictionary). From the discussion above, the C=C bond adds significantly to the stopping power near the peak of the stopping. SRIM calculates that the bonding correction is +6.6%. In this case the two corrections work opposite to each other. The phase-change correction for hydrogen reduces the stopping, while the bond correction increases the stopping. The total adjustment to the stopping is about 6%, and it brings the calculation into reasonably accurate agreement with the data for both H and He ions. The citations of the plotted data are listed below under target of Styrene.
|
He into HC Gases |
Another example shows the stopping of He into Hydrocarbon Gases. A wide variety of gases are shown, ranging from the simple molecule, C2H4 (ethylene) to the very complex molecule C5H10O (3-pentanone). In all cases a significant correction is required to go from the simple Bragg's rule of additivity to the corrected curves. The corrections involve a phase change for the carbon atoms (from solid to gas phase) and bonding corrections which range from 3.3% to 8.3%. All of the data is from the papers of D. Powers (Baylor Univ., USA).
For ions heavier than He, experimental data is sparse. Typical data is for Li ions in Polymer Solids such as polyimide, formvar and polysulfone. These compounds are complex and the SRIM calculation is shown only with the necessary phase correction for converting H, N and O stopping powers to equivalent solid phase stopping. Compounds such as these may show a range of stoichiometries. For example, Formvar is normally quoted as being C5H8O2, while the authors quote their target as C5.56H7.7O2. Since this formulation is from the manufacturer, it is used for the SRIM calculation. But such non-integer stoichiometries prevents the use of any Core and Bond corrections.
|
Li Ions |
|
Figure 4 |
Further details can be found at : Core and Bond Details.
Note: These plots were all made using SRIM-2006. Later versions may have slight variations, always under 2%.
Citations for
Compound Stopping and Ranges
More than 400 papers have looked at the effects of bonding in compounds on the stopping and range of ions in matter. Below are links to collections of citations which have measured various compounds. These citations contain notes which use the abbreviations: R = Ranges, dR = Range Straggling, S = Stopping Powers, dS = Straggling in Stopping.
All files are in Adobe Acrobat format and are about 150-220kB (www.adobe.com/products/acrobat/readstep2.html). The Acrobat Reader does not work well with all browsers. If you have trouble viewing the files below in your browser window, right-click on the link and Save it to your hard disk. Then use your local copy of Acrobat Reader to view and print the file. Acrobat usually works OK on files on your own computer, where you don't have to look at the file in a browser format..
(Go to Citations for Elemental Targets)
If you know of papers which are omitted from these lists, please send the reference to Ziegler@SRIM.org.
---
Papers with Emphasis on Special Targets ---
Targets
|
|
|
|
|
|
|
|
|
|
Air
|
H ions
|
He ions
|
C ions
|
N ions
|
O ions
|
Ne ions
|
Ar ions
|
Kr ions
|
Xe ions
|
Dielectrics
|
H ions
|
He ions
|
C ions
|
N ions
|
O ions
|
Ne ions
|
Ar ions
|
Kr ions
|
Xe ions
|
HydroCarbons
|
H ions
|
He ions
|
C ions
|
N ions
|
O ions
|
Ne ions
|
Ar ions
|
Kr ions
|
Xe ions
|
Phase
Change
|
H ions
|
He ions
|
C ions
|
N ions
|
O ions
|
Ne ions
|
Ar ions
|
Kr ions
|
Xe ions
|
--- Compound Targets ---
|
|
|||||||
|
|
|||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
Note: Details about the chemical composition of many of these compounds (and all of the polymers) can be found in the Compound Dictionary in the SRIM program.
� Lexan, Makrofol and Polycarbonate are usually considered the same material.
� Mylar and Melinex are usually considered the same material.
� Polyimide and Kapton are usually considered the same material.
� PMMA Photoresist is Polymethyl Methacrylate, and is similar to Lucite.
--- Unusual Targets ---
It is possible to put almost anything into a beam of ions.
Below is a table of materials which have been studied
once.
|
|
|
|
|
The above tables can be grouped into materials with similar usage:
Nuclear
Materials
|
||||||||
Semiconductor Materials
|
||||
|
|
||||
|
|
||||
Request for Collaborators
Would you like help in expanding this database and becoming one of its Contributors? We need to expand the stopping of ions in Compounds by including plots of all experiments for ion stopping and ranges in compounds. We need contributors to assume responsibility for any of the Compounds listed above, and to digitize the published stopping powers in a simple Excel worksheet. You will need access to a University Library that contains scientific journals. If you are interested, write to Ziegler@SRIM.org and suggest which compounds that you want. You will receive a simple instruction page and a formatted Excel page. Your name will be permanently displayed with the plot in the future.
![]()
![]()
Further examples of compound effects will be included in this page in future updates.